阅读数:150 评论数:0

1、变换与坐标系

<投影矩阵>*<视图矩阵>*<模型矩阵>*<顶点坐标>

相乘的顺序不能改变。物体本身拥有一个坐标系，叫本地坐标系。把物体放到世界坐标系中，采用了模型矩阵，就是执行缩放、平移、旋转操作的过程。此时物体就具有了世界坐标系。 再加入上帝之眼，就是视图矩阵，包括视点坐标，观察点坐标，和上方向。现在只差最后一步–投影矩阵，物体就可以呈现出来了。 目前显示设备都是二维平面的，所以需要投影矩阵来转换物体。投影矩阵通常分为平行投影和透视投影。

2、模型矩阵

将点的初始位置的坐标P映射到平移、旋转、缩放后的位置坐标P’，即：

$\left[ \begin{aligned} &x\\&y\\&z \end{aligned}  \right] \longrightarrow \left[ \begin{aligned} &\acute{x}\\&\acute{y}\\&\acute{z} \end{aligned}  \right]$

（1）平移变换

$ \left[ \begin{aligned} &\acute{x}\\&\acute{y}\\&\acute{z} \end{aligned}  \right] = \left[ \begin{aligned} &x\\&y\\&z \end{aligned}  \right]  +\left[  \begin{aligned} &t_x\\&t_y\\&t_z  \end{aligned} \right]$

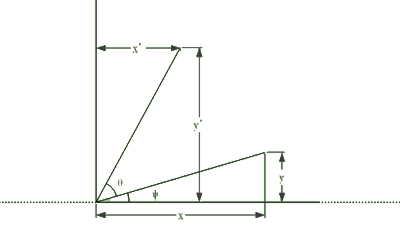
（2）旋转变化

设置线段长度为L

$x = L\cos(\phi)$

$y = L\sin(\phi)$

$\acute{x} = L\cos(\phi+\theta)$

$\Rightarrow L\cos(\phi)\cos(\theta)-L\sin(\phi)\sin(\theta)$

$\Rightarrow x\cos(\theta)-y\sin(\theta)$

$\acute{y} = L\sin(\phi+\theta)$

$\Rightarrow L\sin(\phi)\cos(\theta)+L\cos(\phi)\sin(\theta)$

$\Rightarrow y\cos(\theta)+xsin(\theta)$

使用矩阵表达

$\left[ \begin{aligned} &\acute{x}\\&\acute{y} \end{aligned}\right] = \left[ \begin{aligned} &\cos(\theta)  &-\sin(\theta)\\&\sin(\theta) &\cos(\theta)  \end{aligned} \right] \left[ \begin{aligned} &x\\&y\end{aligned}\right]$

推广到三维空间中

点绕z轴旋转：

$\left[ \begin{aligned} &\acute{x}\\&\acute{y}\\&\acute{z} \end{aligned}\right] = \left[ \begin{array}{3} \cos(\theta)  &-\sin(\theta) &0\\ \sin(\theta) &\cos(\theta) &0\\ 0 &0 &1  \end{array} \right] \left[ \begin{aligned} &x\\&y\\&z \end{aligned}\right]$

点绕x轴旋转

$\left[ \begin{aligned} &\acute{x}\\&\acute{y}\\&\acute{z} \end{aligned}\right] = \left[ \begin{array}{3} 1 &0 &0 \\ 0 &\cos(\theta) &-\sin(\theta) \\ 0 &\sin(\theta) &\cos(\theta)  \end{array} \right] \left[ \begin{aligned} &x\\&y\\&z \end{aligned}\right]$

点绕y轴旋转

$\left[ \begin{aligned} &\acute{x}\\&\acute{y}\\&\acute{z} \end{aligned}\right] = \left[ \begin{array}{3}  \cos(\theta) &0 &-\sin(\theta) \\ 0 &1 &0 \\ \sin(\theta) &0 &\cos(\theta)  \end{array} \right] \left[ \begin{aligned} &x\\&y\\&z \end{aligned}\right]$

（3）缩放变化

$\left[ \begin{aligned} &\acute{x}\\&\acute{y}\\&\acute{z} \end{aligned}\right] = \left[ \begin{array}{3}  s_x &0 &0\\ 0 &s_y &0 \\ 0 &0 &s_z  \end{array} \right] \left[ \begin{aligned} &x\\&y\\&z \end{aligned}\right]$

平移变换，变换后点坐标等于初始位置点坐标加上一个平移向量；而旋转变换和缩放变换，变换后点坐标等于初始位置点坐标乘以一个变换矩阵。

$\acute{P} = P+T, \acute{P}=R\cdot P, \acute{P}=S\cdot P$

使用齐次坐标后，平移变化也可以表示成初始位置坐标左乘一个变换矩阵的形式，它使用4个分量来表示三维空间中的点，前三个分量和普通坐标一样，第四个分量为1。

$\left[ \begin{aligned} &x\\&y\\&z \end{aligned}  \right] \longrightarrow \left[ \begin{aligned} &\acute{x}\\&\acute{y}\\&\acute{z}\\&1 \end{aligned}  \right]$

矩阵有一个性质：

$M\cdot (A\cdot B) = (M\cdotA)\cdot B$

模型矩阵之所以称之为“模型矩阵”，是因为该矩阵与点的位置没有关系，仅仅包含了一系列变换的信息。而在三维世界中，一个模型里所有的顶点往往共享同一个变换，对应同一个模型矩阵。

齐次坐标还有一个优点，能够区分点和向量：在普通坐标里，点和向量都是由三个分量组成的，表示位置的点坐标（2，3，4）和表示方向的向量（2，3，4）没有区别。而在齐次坐标中，第四个分量可以区分它们，点坐标的第四个分量为1，而向量坐标第四个分量为0。

3、视图矩阵

在模型矩阵中，我们关心的是空间中的点在经历变换后在世界坐标系下的位置。事实上，我们更加关心空间中的点相对于观察者的位置。最简单的方案是将观察者置于原点处，面向z轴（或x轴、y轴）正半轴，那么空间中的点在世界坐标系下的位置就是其相对于观察者的位置。

视图矩阵同样也可以分为平移、旋转和缩放，视图矩阵是将观察者视为一个模型，获得的观察者在世界中变换的模型矩阵的逆矩阵。

4、投影矩阵

投影矩阵则将这些顶点坐标映射到二维的屏幕上，即：

$\left[ \begin{aligned} &x\\&y\\&z\\&1 \end{aligned}  \right] \longrightarrow \left[ \begin{aligned} &\acute{x}\\&\acute{y} \end{aligned}  \right]$

最主要的有两种投影方式，正射投影和透视投影。前者用于精确制图，如工业零件侧视图或建筑物顶视图，从屏幕上就可以量测平行于屏幕的线段长度；后者用于模拟视觉，远处的物体看上去较小。

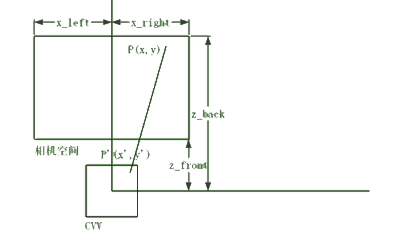
三维世界的显示中，屏幕模拟了一个窗口，你透过这个窗口观察“外面”的世界。你的屏幕是有边缘的（除非你有一个球形的房间，内壁全是屏幕），因此你仅仅能观察到那个世界的一部分，即“相机空间”。相机空间的左、右、上、下边界是受限于屏幕的边缘，同时也设定前、后边界，因为你很难看清太近或太远的东西。在正射投影中，相机空间是一个规则的立方体，而在透视投影中则是一个方台体。

（1）正射投影

定义一个规范的视窗区域（CCV），为x，y，z都处在区间[-1,1]之间的边长为2的立方体。x和y坐标值用来线形拉伸到到实际屏幕上，而z值存储了“深度”。而投影的过程就是将三维空间中的点从相机空间映射到CCV中。

正射投影非常简单，直接将矩形的相机空间线形压缩到CCV中即可。采取顶视图，相机空间的左右边界为 $x_{left}$ 和 $x_{right}$ :

$\dfrac{x-x_{left}}{x_{right}-x_{left}} = \dfrac{\acute{x}-(-1)}{1-(-1)}$

$\Rightarrow \acute{x} = \dfrac{2}{x_{right}-x_{left}}\cdot x - \dfrac{x_{right}+x_{left}}{x_{right}-x{left}}$

推广到y轴和z轴：

$\left[ \begin{aligned} \acute{x}\\ \acute{y} \\ \acute{z} \\ 1 \end{aligned}\right] = \left[ \begin{array}{4}  \dfrac{2}{x_{right}-x_{left}} &0 &0 &-\dfrac{x_{right}+x_{left}}{x_{right}-x_{left}}\\ 0 &\dfrac{2}{y_{top}-x_{bottom}}  &0 &-\dfrac{y_{top}+y_{bottom}}{y_{top}-y_{bottom}}\\ 0 &0 &\dfrac{2}{z_{back}-z_{front}} &-\dfrac{z_{back}+z_{front}}{z_{back}-z_{front}} \\ 0 &0 &0 &1  \end{array} \right] \cdot \left[ \begin{aligned} x\\ y \\ z \\ 1 \end{aligned}\right]$

（2）透视投影

透视投影相对较为复杂

$\left[ \begin{aligned} z\cdot \acute{x}\\ z\cdot \acute{y} \\ z\cdot \acute{z} \\ z \end{aligned}\right] = \left[ \begin{array}{4}  \dfrac{2}{x_{right}-x_{left}} &0  &-\dfrac{x_{right}+x_{left}}{x_{right}-x_{left}} &0 \\ 0 &\dfrac{2}{y_{top}-y_{bottom}}   &-\dfrac{y_{top}+y_{bottom}}{y_{top}-y_{bottom}} &0 \\ 0 &0 &t_z &s_z \\ 0 &0 &1 &0  \end{array} \right] \cdot \left[ \begin{aligned} x\\ y \\ z \\ 1 \end{aligned} \right]$

透视投影矩阵尾行是（0，0，1，0），这样就将计算得到的坐标的第四个分量赋值为z而不是1。将相机空间左乘投影矩阵后的结果不是一个CCV空间，如果你将这个空间画出来，会发现其仍然是一个方台形。这时进行“透视除法”，将上一步得到的点坐标化为第四个分量为1的标准齐次坐标：

$\left[ \begin{aligned} &\acute{x}\\&\acute{y}\\&\acute{z}\\ &1 \end{aligned}  \right] = \left[ \begin{aligned} z\cdot \acute{x}\\z\cdot \acute{y}\\z\cdot \acute{z}\\ \acute{z} \end{aligned}  \right] \cdot \dfrac{1}{z}$

然后我们直接取齐次坐标中的x’和y’值，并将其线形映射到屏幕上，比如点（0，0）出现在屏幕中央，点（-1，1）出现在屏幕左上角。