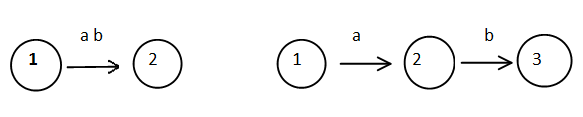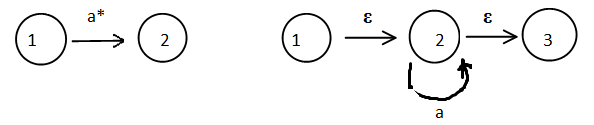形式语言与自动机理论
阅读数:199 评论数:0
跳转到新版页面分类
算法/数据结构
正文
1、简介
(1)编译原理
lex:提取语言中各种保留字、操作符等语言的元素。
yacc:语法分析器
lex和yacc能帮助我们做事情是:用c语言来实现另外一种语言。
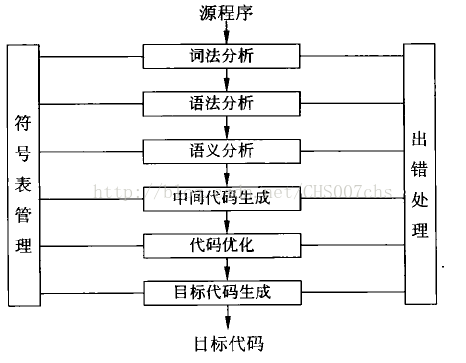
(2)编译器工作原理
对于编译器的各个阶段,在逻辑上可以把它们划分为前端和后端两部分.前端包括从词法分析到中间代码生成各阶段的工作,后端包括中间代码优化和目标代码的生成、优化等。
这样以中间代码为分水岭,把编译器分成了与机器有关的部分和与机器无关的部分。
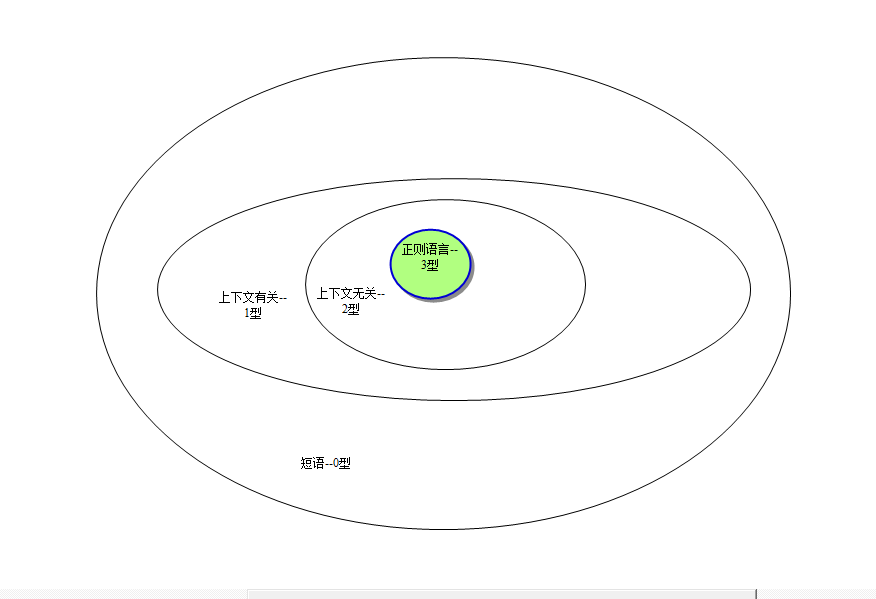
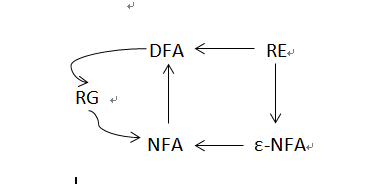
(3)乔姆斯基体系
四大文法的关系:
2、集合关系
(1) 笛卡尔积:AXB,即都分别对应的乘积。
例1-1, A={1,2,3},B={白、黑}
则 AXB={(1,白),(1,黑),(2,白),(2,黑),(3,白),(3,黑)}
(2)幂积:$2^A$,即所有的子集。
例1-2,A={1,2,3},
则$2^A$={ Φ,{1}, {2}, {3}, {1,2}, {1,3}, {2,3}, {1,2,3}}
(3)二元关系:任意的R∈A×B,R是A到B的二元关系
3、句子(前缀)
例2-1,句子abaabb
前缀:ε,a,ab,aba,abaa,abaab,abaabb
真前缀:ε,a,ab,aba,abaa,abaab
后缀:ε,b,bb,abb,aabb,baabb,abaabb
真后缀:ε,b,bb,abb,aabb,baabb
4、文法的构造
例3-1,L(G):{ a^n b^n|n,m>0}
S->aSb|ab (n,m>=0时,S->aSb|ε )
例3-2,L(G): {a^n b^n a^m b^m|n,m>=0}
S->AB A->aAb|ε B->aBb|ε
5、自动机
(1)确定的有穷状态自动机DFA。
- 初态唯一,终态可有多个。
- 任意状态任意射出弧上的元素均不相等
- 识别对象为空时,初态为终态。
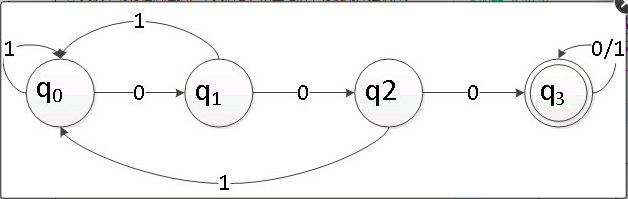
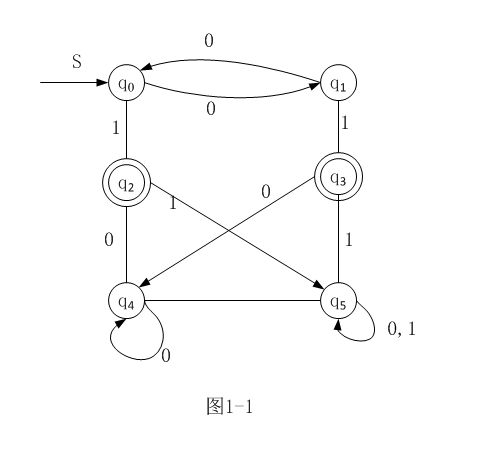
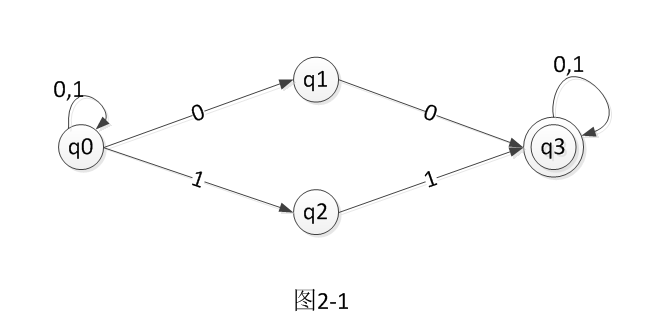
构造:例4-1,L={x000y|x,y ∈{0,1}* }
最小化:
扫描所有的状态对,找出所有的可区分的状态对,不可取分的状态对一定是等价的。
(2)不确定的有穷状态自动机NFA。
- 初态不唯一
- 同一状态射出弧上的标记可以相同
- 初态可以为终态
(3)ε-NFA
是在NFA的基础上,允许直接根据当前状态变换到新的状态而不考虑输入带上的符号
(4)等价性
- NFA与DFA等价、ε-NFA与NFA等价(NFA与DFA等价,ε-NFA与NFA等价,统称它们为FA)
- FA与正则文法等价(FA和左线性文法、右线性文法等价)
对于一个输入字符,NFA与DFA的差异是前者可以进入若干个状态,而后者只能进入一个唯一的状态。虽然从DFA看待问题的角度来说,NFA在某一时刻同时进入若干个状态,但是,这若干个状态合在一起的“总效果”相当于它处于这些状态对应的一个“综合状态”。
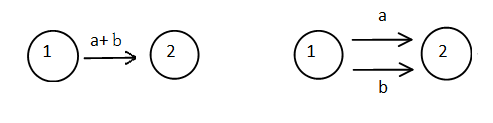
6、正则表达式RE与FA的转换规则
7、正则表达式RL
(1)封闭性
- 正则语言的并、交、补是正则语言。
- 正则语言的乘积(连接)是正则语言。
- 正则语言的差是正则语言。
- 正则语言的闭包是正则语言。
- 正则语言的商是正则语言。
- 正则语言的同态是正则语言。
- 正则语言的逆转是正则语言。
(2)泵引理
DFA在处理一个足够长的句子的过程中,必定会重复地经过某一个状态。换句话说,在DFA的状态转移图中,必定存在一条含有回路的从启动状态到某个终止状态的路。由于是回路,所以,DFA可以根据实际需要沿着这个回路循环运行,相当于这个回路中弧上的标记构成的非空子串可以重复任意多次。
(3)等价模型
8、上下文无关语言CFL
(1)封闭性
- 并、乘积、闭包是封闭的
- 交、补不封闭
(2)语法树
- 每个句型至少存在一颗语法树,每颗语法树至少存在一个推导。
- 每颗树的叶子组成句型(句型就是我们的结果)。
- 每颗简单子树的叶子组成简单短语。
- 最左简单子树的叶子组成句柄。
(3)CFG的化简
- 去无用符号:首先删除不可终止的,再删除不可到达的。
- 去空产生式:先求可空变量,再看空产生式会对哪些产生式有影响
- 去单一产生式:可能会产生新的无用符号或单一产生式。
9、图灵机与计算机
(1)用计算机模拟图灵机,不是任何的图灵机都能被计算机来模拟
(2)图灵机比计算机速度慢
9、几中不同的转换
(1)DFA的最小化
DFA最小化,最简单的理解就是“劈枝斩叶留主干”,最小化的DFA比原状态等价且状态数少。
劈枝斩叶留住干,在化简时候就是对等价的状态进行合并。
那么怎么找等价状态呢?所有的终结符号都是等价的。这也是找之后等价符号的基础。详情看下面例子。
化简步骤:
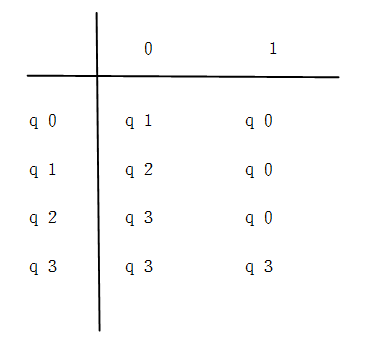
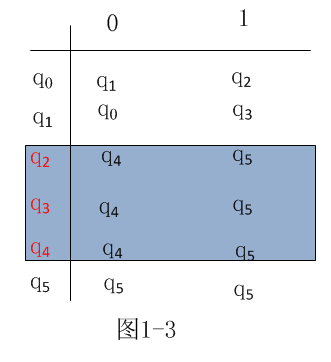
A 画出状态矩阵图
B 找终结符(等价的)
C 根据找到的等价的终结符,在继续找其他的等价符号。
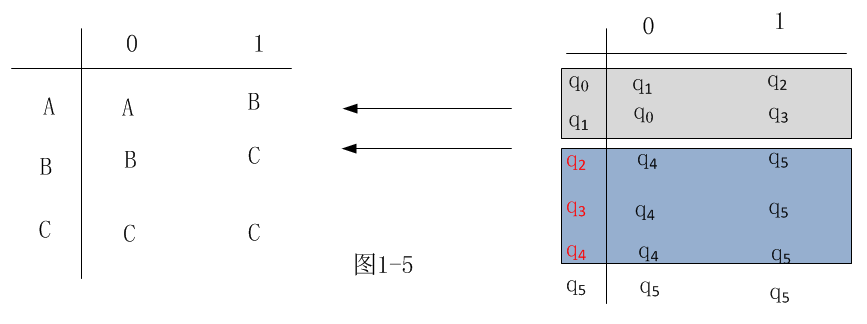
D 转换。如图示
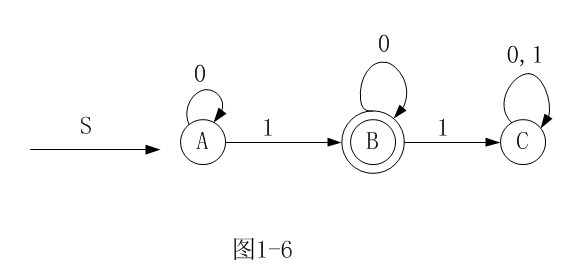
E 所得到的最小状态的DFA
(2)NFA -》DFA的转换
A 给定的NFA为图
B 写I , I0 ,I1
C 写I={q0}开始符号
D 求I0 ,I1
E 所有包含终态的都是终态
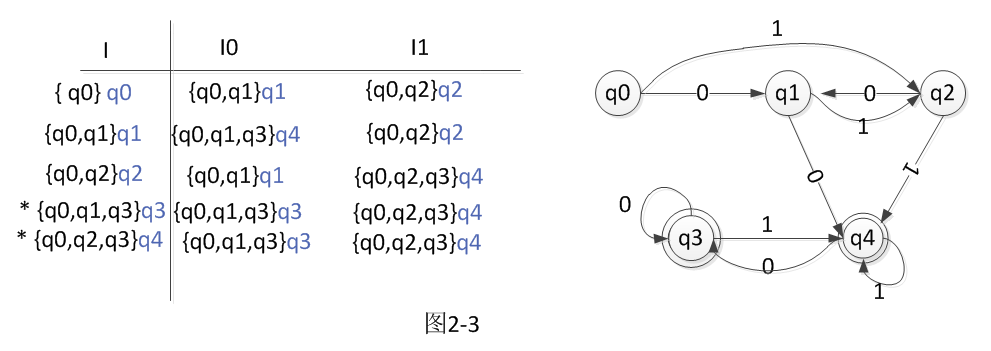
NFA的矩阵如图示
转换图
总结:I 的第一个是开始符号q0,第二第三个就是上一个中的跟之前的I 不相同的。
直到I中将所有的I0,I1都包括了,就停止了。
(3)带空移动的NFA到NFA
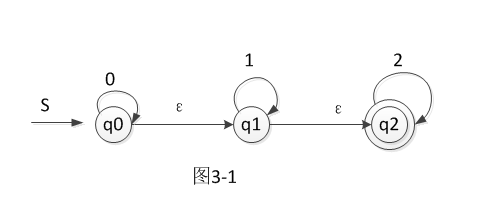
带空的NFA如图3-1示
转换为等价的NFA的步骤:
A 类似NFA转换到DFA的第一步,不同的是,左侧的第一个是开始符号q0以及q0和空之后的所有字符。 例:图3-1的第一个就是{q0,q1,q2}
B 第二步是找第二个字符,及所有的所能识别的空移动到达的字符。
C 之后的以此类推,直到所有的字符都出现。
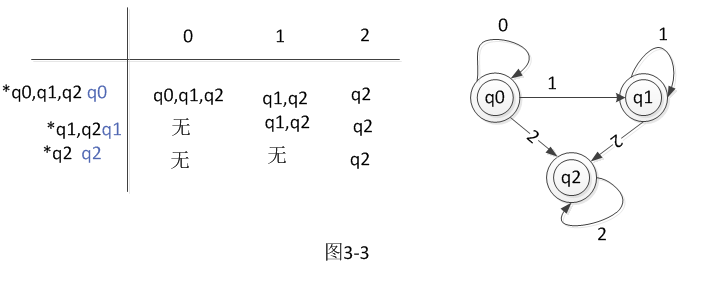
转换图如3-2所示
等价的NFA为图3-3所示
总结:带空的NFA到NFA与NFA到DFA的不用是左侧的符号,NFA到DFA左侧符号不能很方便的看出来,得根据右侧,第一个就是一个开始符号,空NFA到NFA左侧是所有的符号及识别空所能到达的符号,第一个符号是开始符号或者是开始符号和识别空所到达的符号。
(4)词法分析器的构造
有了下正规式和有限自动机的理论基础后,就可以构造出编译 程序的词法分析模块:
- 用正规式描述语言中的单词构成规则
- 为每个正规式构造一个NFA,它识别正规式所表示的正规集
- 将构造出的NFA转换成等价的DFA
- 对DFA进行最小化处理,使其最简
- 从DFA构造词法分析器
(5)语法分析方法
程序设计语言的绝大多数语法规则可以采用上下文无关文法进行描述(2 型文法)
自顶向下语法分析方法:
对于给定的输入串,从文法的开始符号出发进行最左推导,直到得到一个合法的句子或者发现一个非法结构。
- 消除左递归,以避免分析陷入死循环;
- 提取左因子,以避免回溯
自底向上语法分析方法:
也称移进-归约分析法,对输入序列从左向右进行扫描,并将输入符号逐个移进一个栈中,边移进边分析,一旦栈项符号串形成某个句型的可归约串时,就用某个产生式的左部非终结符来替代。重复这一过程,直至栈中只剩下方法的开始符号且输入串也被扫描完时为止,确认输入串是文法的句子,表示分析成功;否则,进行错误处理。