阅读数:101 评论数:0

1、B树

B 树是为了磁盘或其它存储设备而设计的一种多叉平衡查找树。与红黑树很相似，但在降低磁盘I/0操作方面要更好一些。 B树与红黑树最大的不同在于，B树的结点可以有许多子女，从几个到几千个。那为什么又说B树与红黑树很相似呢?因为与红黑树一样，一棵含n个结点的B树的高度也为O（lgn），但可能比一棵红黑树的高度小许多，应为它的分支因子比较大。所以，B树可以在O（logn）时间内，实现各种如插入（insert），删除（delete）等动态集合操作。

（1）定义

一棵m阶的B树特性如下：

1. 树中每个结点最多含有m个孩子（m>=2）
2. 除根结点和叶子结点外，其它每个结点至少有$\lfloor \dfrac{m}{2} \rfloor $个孩子；
3. 若根结点不是叶子结点，则至少有2个孩子（特殊情况：没有孩子的根结点，即根结点为叶子结点，整棵树只有一个根节点）
4. 所有叶子结点都出现在同一层.
5. 有k个孩子的非叶子结点恰好有k-1个关键字

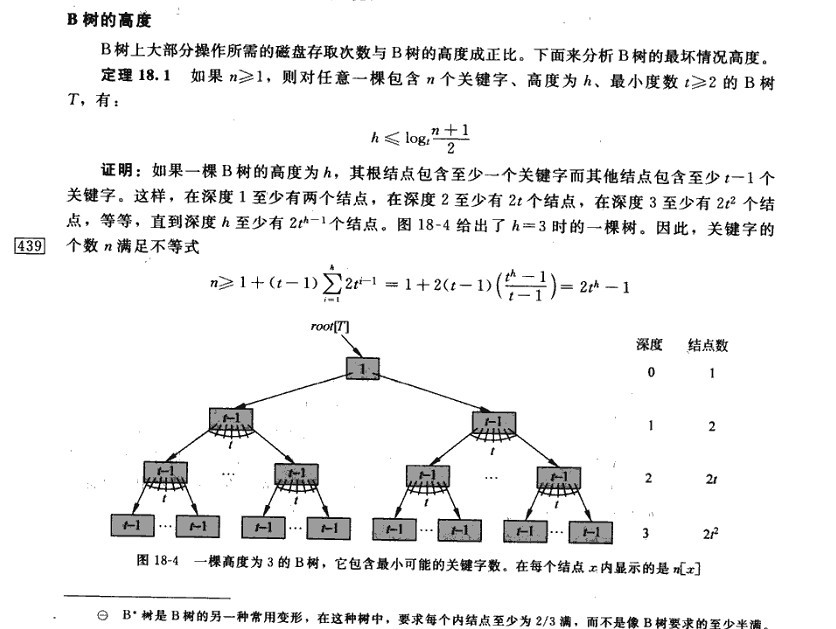
（2）B树的高度

2、B+树

是应文件系统所需而产生的一种B-tree的变形树。

一棵m阶的B+树和m阶的B树的异同点在于：

（1）有n棵子树的结点中含有n-1 个关键字； (与B 树n棵子树有n-1个关键字 保持一致）

（2）所有的叶子结点中包含了全部关键字的信息，及指向含有这些关键字记录的指针，且叶子结点本身依关键字的大小自小而大的顺序链接。（而B 树的叶子节点并没有包括全部需要查找的信息)

（3）所有的非终端结点可以看成是索引部分，结点中仅含有其子树根结点中最大（或最小）关键字。 (而B 树的非终节点也包含需要查找的有效信息)