阅读数:189 评论数:0

一、概述

在机器学习中，我们经常需要计算样本之间的相似度。

二、欧式距离 （Euclideam Distance）

欧式距离可以解释为连接两个点的线段的长度，使用勾股定理之这些点的笛卡尔坐标计算距离。

$$D(x,y)=\sqrt{\sum_{n-1}^n (x_i-y_i)^2 }$$

尽管这是一种常用的距离度量，但欧式距离并不是尺度不变的，这意味着所计算的距离可能会根据特征的单位发生倾斜。通常，在使用欧式距离度量之前，需要对数据进行归一化处理。

此外，随着数据维数的增加，欧氏距离的作用也就越小。这与维数灾难（curse of dimensionality）有关。

二、曼哈顿距离（Manhattan Distance）

曼哈顿距离通常称为出租车距离或城市街区距离，用来计算实值向量之间的距离。想象一下均匀网格棋盘上的物体，如果它们只能移动直角，曼哈顿距离是指两个向量之间的距离，在计算距离时不涉及对角线移动。

$$D(x,y)=\sum_{n-1}^n| (x_i-y_i)|$$

尽管曼哈顿距离在高维数据中似乎可以工作，但它比欧式距离直观性差，尤其是在高维数据中使用时。此外，由于它可能不是最短路径，有可能比欧氏距离给出一个更高的距离值。

三、切比雪夫距离（Chebyshev Distance）

切比雪夫距离定义为两个向量在任意坐标维度上的最大差值。换句话说，它就是沿着一个轴的最大距离。切比雪夫距离通常被称为棋盘距离，因为国际象棋的国王从一个方格到另一个方格的最小步数等于切比雪夫距离。

$$D(x,y)=max_{i}| (x_i-y_i)|$$

在实践中，切比雪夫距离经常用于仓库物流，因为它非常类似于起重机移动一个物体的时间。

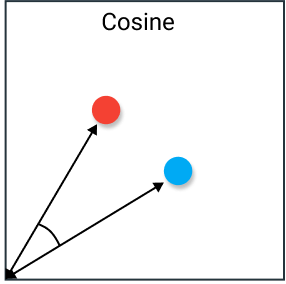
四、余弦相似度（Cosine Similarity）

余弦相似度是指两个向量夹角的余弦。如果将向量归一化为长度均为 1 的向量，则向量的点积也相同。

两个方向完全相同的向量的余弦相似度为 1，而两个彼此相对的向量的余弦相似度为 - 1。注意，它们的大小并不重要，因为这是在方向上的度量。

$$D(x,y)=cos(\theta)=\dfrac{x \cdot y}{||x||y||}$$

余弦相似度的一个主要缺点是没有考虑向量的大小，而只考虑它们的方向.

五、马氏距离（Mahalanobis distance）

马氏距离在欧式距离的计算基础上增加了协议差矩阵，后面学习一下矩阵论再补充。