阅读数:52 评论数:0

一、在线段“旋转”中解释两个“为什么”

1、为什么正弦量可以用复数来表示？

正弦量用复数表示的推理过程与正弦函数图像的形成过程是相通的，运用相似的“旋转”原理。

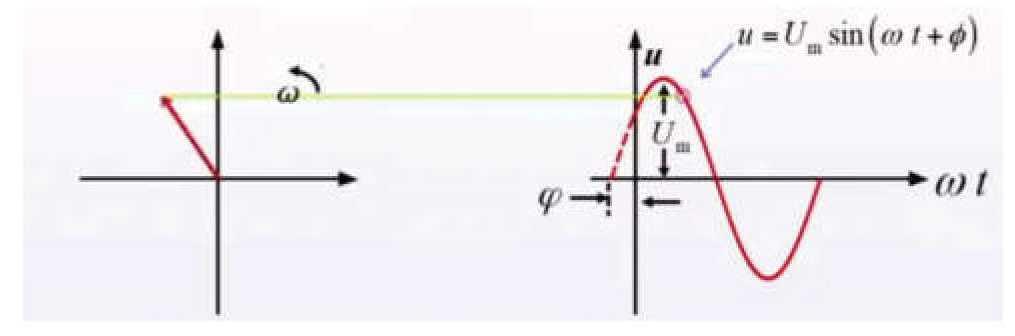
设有正弦电压$u(t)=u_m sin(\omega t+\varphi)$，在左边直角坐标系中取长度为$u_m$有向线段，初始位置与x轴正方向的夹角为$\varphi$，并以角频率$\omega$作逆时针旋转。则旋转有向线段任一时刻在纵轴上的投影值刚好对应正弦量在该时该的顺时值。因为旋转的有向线段里面包含了正弦量的三个特征值，长度是正弦量的振幅$u_m$，初始位置是正弦量的初相$\varphi$，而旋转的角频率是$\omega$，可见一个旋转的有向线段可以表示一个正弦量。

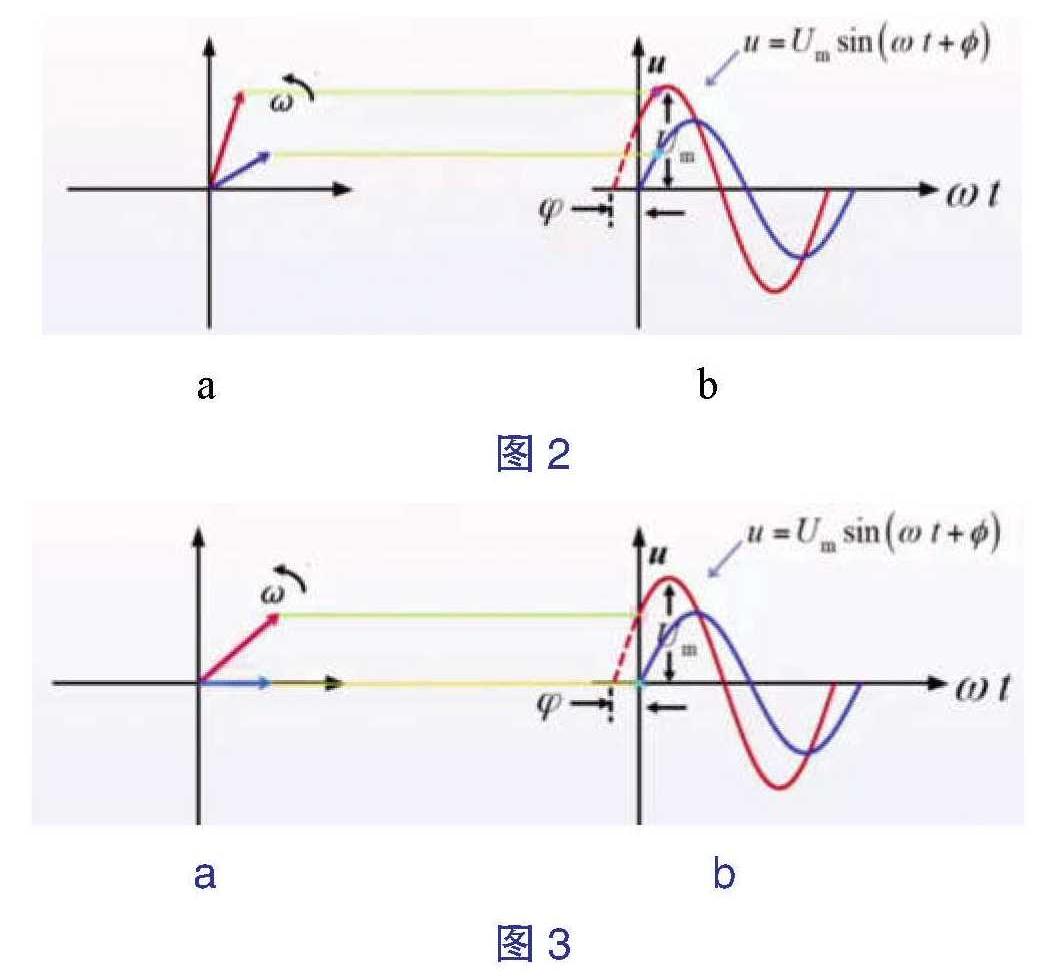
如果有两个正弦量，就可以在坐标里面画出两个有向线段，如图2。由于在同一正弦稳态电路中，正弦量频率都是相同的，所以同频率的旋转有向线段的相对位置是不变的，让旋转的有向线段固定在初始位置，如图3。而固定的有向线段可用复数表示，所以正弦量也可用复数来表示，复数的模即为正弦量的幅值 ，辐角即为正弦量的初相位。如$u(t)=u_m sin(\omega t+\varphi)$可以表示为复数$u_m=u_m\angle \varphi $

2、为什么线圈切割磁感线形成正弦交流电？

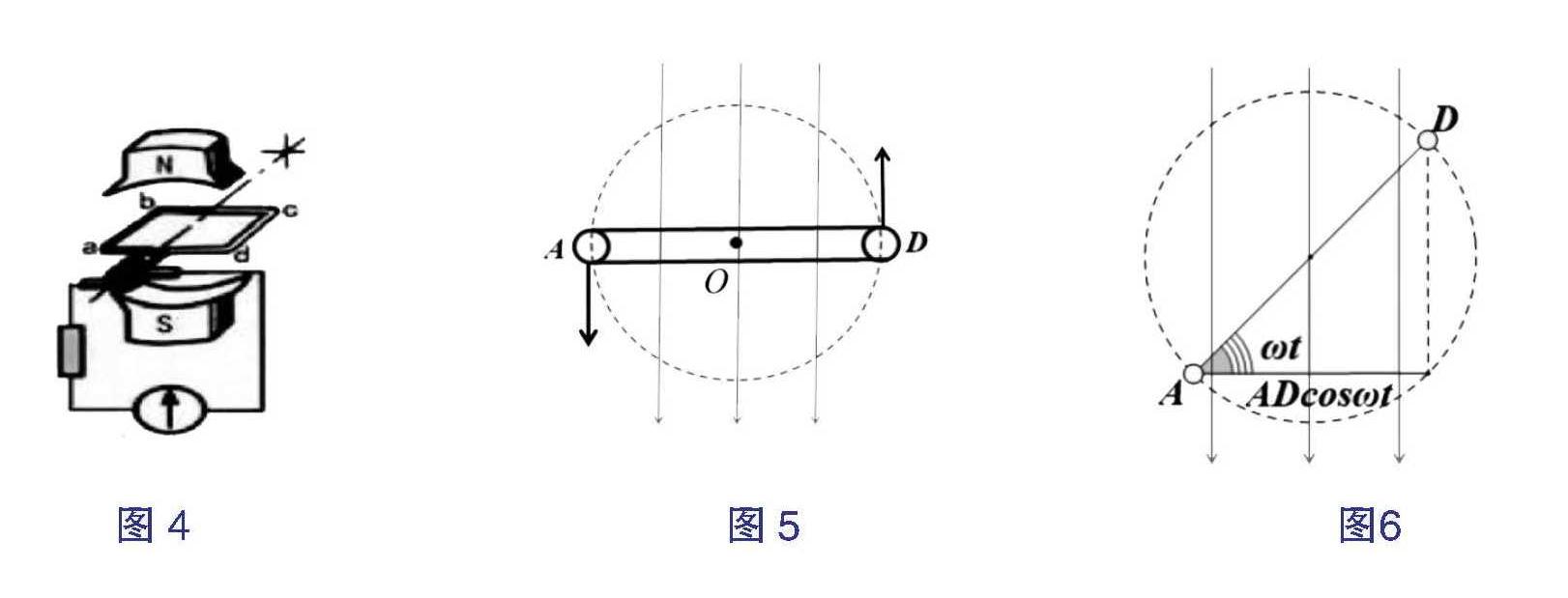
闭合线圈在匀强磁场中绕垂直于磁感线的轴线匀速运动，从正前方观察线圈，只能看到线圈的AD边。我们可以看成线段AD绕着O点以角速度$\omega$ 做逆时针旋转如图5，线圈与水平右方向的夹角为$\omega t$，AD在水平方向的投影为AD$cos\omega t$如图6，而AB长度保持不变，线圈的面积为S，因此线圈在垂直方向的投影面积为$AB\cdot AD\cos \varphi=S\cos\omega t$，因此穿过线圈的平面的磁通量$\Phi=BS\cos\omega t$，根据法拉利电子感应定律，结合导数知识，感应电动势$e=n\dfrac{\triangle \Phi}{\triangle t}=n{\Phi}^{'}=-nBS\omega \sin\omega t$。

从数据角度分析，由于$e=-nBS\omega\sin\omega t$，当线圈处于水平位置时，$\sin\omega t=0,e=0$，而当线圈处于垂直位置时$\sin\omega t=0,e=-nBS\omega$，取得最值；从物理角度分析，当线圈处于中性面位置时，由于力矩的方向平行于磁力线的方向，无切割磁力线的运动，此处感应电动势为0；而当线圈处于垂直位置时，两边都垂直切割磁感线，此时感应电动势最大。

由此思想，可以证明线圈切割磁感线形成的交流电可以用一个正弦函数来表示。