阅读数:81 评论数:0

Trie，又称单词查找树或键树，是一种树形结构，是一种哈希树的变种。其高效率是以空间为代价的.

性质：

（1）根节点不包含字符，除根节点外每一个节点都只包含一个字符

（2）从根节点到某一节点，路径上经过的字符连接起来，为该节点对应的字符串

（3）每个节点的所有子节点包含的字符都不相同

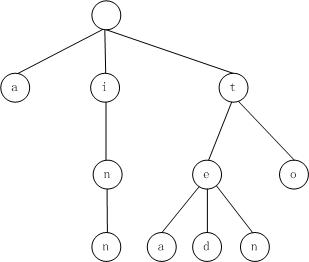
例如，单词序列a, to, tea, ted, ten, i, in, inn，对应的trie：

下面以英文单词构建的字典树为例，这棵Trie树中每个结点包括26个孩子结点，因为总共有26个英文字母(假设单词都是小写字母组成)。

    则可声明包含Trie树的结点信息的结构体:

#define MAX 26
 
typedef struct TrieNode               //Trie结点声明 
{
    bool isStr;                      //标记该结点处是否构成单词 
    struct TrieNode *next[MAX];      //儿子分支 
}Trie;

Trie的操作

在Trie树中主要有3个操作，插入、查找和删除。一般情况下Trie树中很少存在删除单独某个结点的情况，因此只考虑删除整棵树。

（1）插入

假设存在字符串str，Trie树的根结点为root。i=0，p=root。

  1)取str[i]，判断p->next[str[i]-97]是否为空，若为空，则建立结点temp，并将p->next[str[i]-97]指向temp，然后p指向temp；

   若不为空，则p=p->next[str[i]-97]；

  2)i++，继续取str[i]，循环1)中的操作，直到遇到结束符'\0'，此时将当前结点p中的isStr置为true。

（2）查找

假设要查找的字符串为str，Trie树的根结点为root，i=0，p=root

  1)取str[i]，判断判断p->next[str[i]-97]是否为空，若为空，则返回false；若不为空，则p=p->next[str[i]-97]，继续取字符。

  2)重复1)中的操作直到遇到结束符'\0',若当前结点p不为空并且isStr为true，则返回true，否则返回false。

（3）删除

删除可以以递归的形式进行删除。

/*Trie树(字典树) 2011.10.10*/
 
#include <iostream>
#include<cstdlib>
#define MAX 26
using namespace std;
 
typedef struct TrieNode                     //Trie结点声明 
{
    bool isStr;                            //标记该结点处是否构成单词 
    struct TrieNode *next[MAX];            //儿子分支 
}Trie;
 
void insert(Trie *root,const char *s)     //将单词s插入到字典树中 
{
    if(root==NULL||*s=='\0')
        return;
    int i;
    Trie *p=root;
    while(*s!='\0')
    {
        if(p->next[*s-'a']==NULL)        //如果不存在，则建立结点 
        {
            Trie *temp=(Trie *)malloc(sizeof(Trie));
            for(i=0;i<MAX;i++)
            {
                temp->next[i]=NULL;
            }
            temp->isStr=false;
            p->next[*s-'a']=temp;
            p=p->next[*s-'a'];   
        }   
        else
        {
            p=p->next[*s-'a'];
        }
        s++;
    }
    p->isStr=true;                       //单词结束的地方标记此处可以构成一个单词 
}
 
int search(Trie *root,const char *s)  //查找某个单词是否已经存在 
{
    Trie *p=root;
    while(p!=NULL&&*s!='\0')
    {
        p=p->next[*s-'a'];
        s++;
    }
    return (p!=NULL&&p->isStr==true);      //在单词结束处的标记为true时，单词才存在 
}
 
void del(Trie *root)                      //释放整个字典树占的堆区空间 
{
    int i;
    for(i=0;i<MAX;i++)
    {
        if(root->next[i]!=NULL)
        {
            del(root->next[i]);
        }
    }
    free(root);
}
 
int main(int argc, char *argv[])
{
    int i;
    int n,m;                              //n为建立Trie树输入的单词数，m为要查找的单词数 
    char s[100];
    Trie *root= (Trie *)malloc(sizeof(Trie));
    for(i=0;i<MAX;i++)
    {
        root->next[i]=NULL;
    }
    root->isStr=false;
    scanf("%d",&n);
    getchar();
    for(i=0;i<n;i++)                 //先建立字典树 
    {
        scanf("%s",s);
        insert(root,s);
    }
    while(scanf("%d",&m)!=EOF)
    {
        for(i=0;i<m;i++)                 //查找 
        {
            scanf("%s",s);
            if(search(root,s)==1)
                printf("YES\n");
            else
                printf("NO\n");
        }
        printf("\n");   
    }
    del(root);                         //释放空间很重要 
    return 0;
}