阅读数:416 评论数:0

一、介绍

1、二分图

其最大的特点在于，可以将图里的顶点分为两个集合，且集合内的点没有直接关联。

2、增广路径

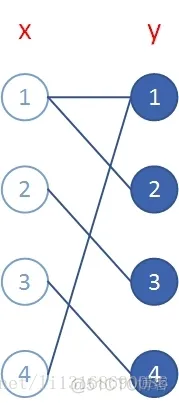
增广路径是指，由一个未匹配的顶点开始，经过若干个匹配顶点，最后到达对面集合的一个未匹配顶点的路径。

二分图最大匹配的经典匈牙利算法是由Edmonds在1965年提出的，算法的核心就是根据一个初始匹配不停的找增广路，直到没有增广路为止。

找增广路的时候既可以采用dfs也可以采用bfs，两者都可以保证O(nm)的复杂度，因为每找一条增广路的复杂度是O(m)，而最多增广n次，dfs在实际实现中更加简短。

二、匈牙利算法

二分图的最大匹配有两种求法，第一种是最大流；第二种就是我现在要讲的匈牙利算法。这个算法说白了就是最大流的算法，但是它跟据二分图匹配这个问题的特点，把最大流算法做了简化，提高了效率。

它的基本模式就是：

初始时最大匹配为空
while 找得到增广路径
    do 把增广路径加入到最大匹配中去

1、二分图中增广路径的性质

1. 有奇数条边。
2. 起点在二分图的左半边，终点在右半边。
3. 路径上的点一定是一个在左半边，一个在右半边，交替出现。
4. 整条路径上没有重复的点。
5. 起点和终点都是目前还没有配对的点，而其它所有点都是已经配好对的。
6. 路径上的所有第奇数条边都不在原匹配中，所有第偶数条边都出现在原匹配中。
7. 最后，也是最重要的一条，把增广路径上的所有第奇数条边加入到原匹配中去，并把增广路径中的所有第偶数条边从原匹配中删除（这个操作称为增广路径的取反），则新的匹配数就比原匹配数增加了1个。

但是要完成匈牙利算法，还需要一个重要的定理：

如果从一个点A出发，没有找到增广路径，那么无论再从别的点出发找到多少增广路径来改变现在的匹配，从A出发都永远找不到增广路径。

有了这个定理，匈牙利算法就成形了。如下：

初始时最大匹配为空
for 二分图左半边的每个点i
 do 从点i出发寻找增广路径。如果找到，则把它取反（即增加了总了匹配数）

如果二分图的左半边一共有n个点，那么最多找n条增广路径。如果图中共有m条边，那么每找一条增广路径（DFS或BFS）时最多把所有边遍历一遍，所花时间也就是m。所以总的时间大概就是O（n * m）。

2、示例：

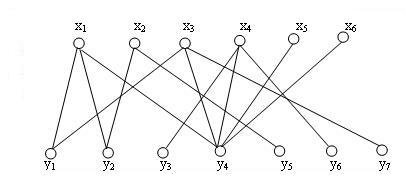
（1）起始没有匹配

（2）选中第一个x点，找到第一根连线

（3）选中第二个点找到第二根连线

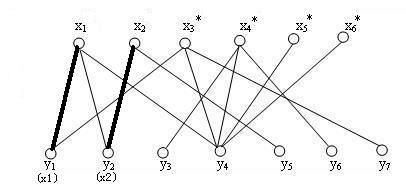
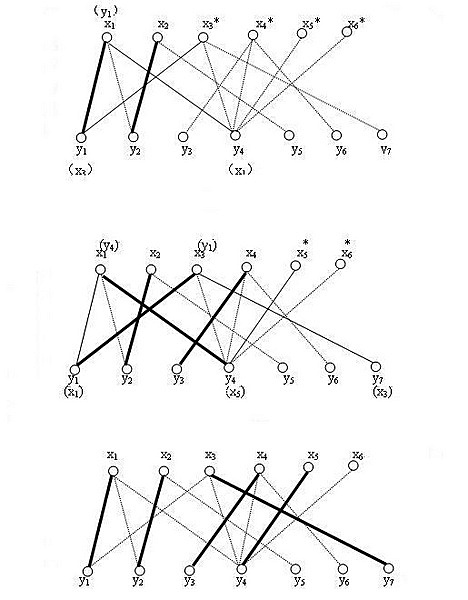
（4）发现x3的第一条边x3y1已经被人占了，找出x3出发的的交错路径x3-y1-x1-y4，把交错路中已在匹配上的边x1y1从匹配中去掉，剩余的边x3y1 x1y4加到匹配中去，同理加入x4、x5。

 匈牙利算法可以深度有限或者广度优先，刚才的示例是深度优先，即x3找y1,y1已经有匹配，则找交错路。若是广度优先，应为：x3找y1,y1有匹配，x3找y2。

三、Hopcroft-Karp算法

1、原理

为了降低时间复杂度，可以在增广匹配集合M时，每次寻找多条增广路径。这样就可以进一步降低时间复杂度，可以证明，算法的时间复杂度可以到达O（$\sqrt((n)\cdot m$）。

该算法的精髓在于同时找多条增广路进行反转。我们先用BFS找出可能的增广路，这里用到BFS层次搜索的概念，记录当前结点在第几层，用于后面DFS沿增广路反转时用，然后再用DFS沿每条增广路反转。这样不停地找，直至无法找到增广路为止。

2、基本算法

该算法主要是对匈牙利算法的优化，在寻找增广路径的时候同时寻找多条不相交的增广路径，形成极大增广路径集，然后对极大增广路径集进行增广。在寻找增广路径集的每个阶段，找到的增广路径集都具有相同的长度，且随着算法的进行，增广路径的长度不断的扩大。可以证明，最多增广n^0.5次就可以得到最大匹配。

算法分为若干阶段，每阶段包含若下步骤：

1. 将左侧未匹配点集设为起点，按照交错路径的条件，BFS，对图分层，在某层出现未匹配的右边点时停止
2. 将左侧未匹配点集设为起点，按照层的顺序，和交错路径的条件，DFS

四、KM算法

对于二分图的每条边都有一个权（非负），要求一种完备匹配方案，使得所有匹配边的权和最大，记做最优完备匹配。（特殊的，当所有边的权为1时，就是最大完备匹配问题）

为每个点设立一个顶标Li，Li=max{wi,j}(i∈x,j∈y)，Lj=0。

定理：二分图中所有vi,j=Li+Lj的边构成一个子图G，用匈牙利算法求G中的最大匹配，如果该匹配是完备匹配，则是最优完备匹配。