阅读数:129 评论数:0

对于某一确定的模，某数减去小于模的另一个数，总可以用该数加上模与另一个数绝对值之差来代替。（这就是为什么可以用补码进行加减运算的原因）

1、原码

原码体现了数据的绝对值。

（1）定点小数的原码定义如下：

$x_{原} = \left\{  \begin{aligned} &x , &0 \le x \lt 1 \\ &1-x等价于1+ |x|, &-1 \lt x \le 0 \end{aligned} \right.$

（2）定点整数的原码

$x_{原} = \left\{  \begin{aligned} &x , &0 \le x \lt 2^{n-1} \\ &2^{n-1}-x, &-2^{n-1} \lt x \le 0 \end{aligned} \right.$

2、补码

（1）定点小数的补码

$x_{补} = \left\{  \begin{aligned} &x , &0 \le x \lt 1 \\ &2+经, &-1 \lt x \le 0 \end{aligned} \right.$

（2）定点整数的补码

$x_{补} = \left\{  \begin{aligned} &x , &0 \le x \lt 2^{n-1} \\ &2^{n}+x, &-2^{n-1} \lt x \le 0 \end{aligned} \right.$

正数的补码与其原码相同，负数补码求解的一个简便方式：符号位不变，数值部分自低向高位搜索，第一个1及其以右的各位0保持不变，以左的各位按位取反。

补码的符号位扩展：

结论1：要将n位纯小数补码变为2n位，只需在末尾添加n个0即可。

结论2：要将整数补码的模扩大$2^n$倍，只需将符号位向左复制n位即可。

补码的算术右移（除2运算）

结论：若已知$x_{补}$求$0.5_{补}$，可将$x_{补}$连同符号位在内右移1位，同时符号位保持不变。

补码的算术左移（乘2运算）

结论：已知$x_{补}$求$2x_{补}$，只需要将$x_{补}$的各位左移1位，末位补0.

3、反码

（1）定点小数的反码

$x_{反} = \left\{  \begin{aligned} &x , &0 \le x \lt 1 \\ &2-2^{-(n-1)}+x, &-1 \lt x \le 0 \end{aligned} \right.$

（2）定点整数的反码

$x_{反} = \left\{  \begin{aligned} &x , &0 \le x \lt 2^{n-1} \\ &2^{n}-1+x, &-2^{n-1} \lt x \le 0 \end{aligned} \right. $

正数的反码与原码相同，负数的反码为该负数对应的原码符号不变，数值位按位取反。

反码加1得到补码。

4、移码

由于浮点数的阶码使用移码，所以只介绍定点整数的移码。

$x_{移} = 2^{n-1}+x$

原码和反码的表示范围相同，补码的移码的表示范围相同(补码里的0只有一种表示，因此多了一个离散状态可以表示其他的数)。

【x】移----》符号取反《---【x】补

实际上，如果机器字长为n，规定偏移量为2^(n-1)，只要将补码的符号位取反便可获取相应的移码表示。

5、浮点数

因为无论采用定点，还是浮点表示，n位编码总是最多只能表示2^n个数，所以采用浮点表示法虽然扩大了表示范围，但没有增加可表示的数值的个数，只是数据间的间隔变稀疏了。

浮点数的表示范围主要由阶码决定，精度则由尾数决定。为了尽可能多地保留有效数字的位数，使有效数字尽量占满尾数数位，通常采用浮点数规格化形式，即将尾数的绝对值限定在某个范围内。

如果阶码的底为2，则规格化浮点数的尾数应满足：

$\dfrac{1}{2} \le |M| \lt 1$

$M \ge 0, M=0.1xxx..x$

$M \lt 0, M=1.0xx..x$

尾数采用补码表示。为了使计算机判断方便，一般不把【-1/2】补（1.1000.000）列为规格化的数，而把【-1】补（1.000.000）列为规格化的数。

（1）IEEE754

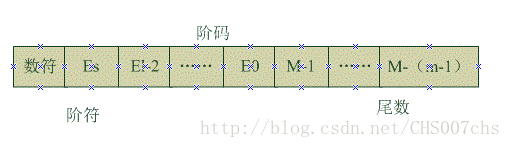
符号位 阶码 尾数 长度
float 1 8 23 32
double 1 11 52 64

在IEEE754标准中，约定小数点左边隐含有一位，通常这位数就是1，因此单精度浮点数尾数的有效位数为24痊，即尾数为1.xxx。

单精度数的偏差值为127，而双精度数的偏差值为1023。偏差的引入； 使得对于单精度数，实际可以表达的指数范围变成-127到128之间（包含两端）。

"当阶码E 为全0且尾数M 也为全0时，表示的真值x 为零，结合符号位S 为0或1，有正零和负零之分。当阶码E 为全1且尾数M 为全0时，表示的真值x 为无穷大，结合符号位S 为0或1，也有+∞和-∞之分。这样在32位浮点数表示中，要除去E 用全0和全1(255)10表示零和无穷大的特殊情况，指数的偏移值不选128(10000000)，而选127(01111111)。对于规格化浮点数，E 的范围变为1到254，真正的指数值e 则为-126到+127。"

6、一些思考

（1）为何要使用原码、反码和补码

首先, 因为人脑可以知道第一位是符号位, 在计算的时候我们会根据符号位, 选择对真值区域的加减. (真值的概念在本文最开头). 但是对于计算机, 加减乘数已经是最基础的运算, 要设计的尽量简单. 计算机辨别"符号位"显然会让计算机的基础电路设计变得十分复杂! 于是人们想出了将符号位也参与运算的方法. 我们知道, 根据运算法则减去一个正数等于加上一个负数, 即: 1-1 = 1 + (-1) = 0 , 所以机器可以只有加法而没有减法, 这样计算机运算的设计就更简单了.

如果用原码表示, 让符号位也参与计算, 显然对于减法来说, 结果是不正确的.这也就是为何计算机内部不使用原码表示一个数.

为了解决原码做减法的问题, 出现了反码。

发现用反码计算减法, 结果的真值部分是正确的. 而唯一的问题其实就出现在"0"这个特殊的数值上. 虽然人们理解上+0和-0是一样的, 但是0带符号是没有任何意义的. 而且会有[0000 0000]原和[1000 0000]原两个编码表示0.

于是补码的出现, 解决了0的符号以及两个编码的问题。

使用补码, 不仅仅修复了0的符号以及存在两个编码的问题, 而且还能够多表示一个最低数. 这就是为什么8位二进制, 使用原码或反码表示的范围为[-127, +127], 而使用补码表示的范围为[-128, 127].

（2）原码、反码、补码的数学原理

同余数的两个定理：

A 反身性

$ a \equiv  a ( mod m)$

B 线性运算定理

$如果 a\equiv b (mod m), c \equiv d (mod m)，那么$

$ a \pm c \equiv b \pm d (mod m)$

$ a * c \equiv b*d (mod m)$

接下来回到二进制的问题上, 看一下: 2-1=1的问题

2-1=2+(-1) = [0000 0010]原 + [1000 0001]原= [0000 0010]反+ [1111 1110]反

先到这一步, -1的反码表示是1111 1110. 如果这里将[1111 1110]认为是原码, 则[1111 1110]原 = -126, 这里将符号位除去, 即认为是126.

发现有如下规律:

    (-1) mod 127 = 126

    126 mod 127 = 126

即：

    (-1) ≡ 126 (mod 127)

    2-1 ≡ 2+126 (mod 127)

2-1 与 2+126的余数结果是相同的! 而这个余数, 正式我们的期望的计算结果: 2-1=1

所以说一个数的反码, 实际上是这个数对于一个模的同余数. 而这个模并不是我们的二进制, 而是所能表示的最大值!

既然反码可以将减法变成加法, 那么现在计算机使用的补码呢? 为什么在反码的基础上加1, 还能得到正确的结果?

2-1=2+(-1) = [0000 0010]原 + [1000 0001]原 = [0000 0010]补 + [1111 1111]补

如果把[1111 1111]当成原码, 去除符号位, 则:

[0111 1111]原 = 127

其实, 在反码的基础上+1, 只是相当于增加了膜的值:

    (-1) mod 128 = 127

    127 mod 128 = 127

    2-1 ≡ 2+127 (mod 128)