阅读数:138 评论数:0

一、坐标系统

1、世界坐标系（world coordinate system）

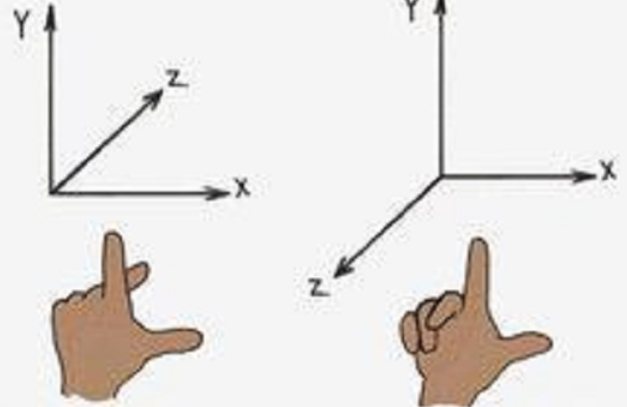
是一个三维坐标系，多用右手直角坐标系，用来描述物体所处理的场景空间。坐标原点在屏幕中心，z轴垂直于屏幕指向屏幕外，y轴竖直向上，x轴水平向右。

2、物体本地坐标系

3、设备坐标（device coordinate system）

是一个二维坐标系，用来表示三维模型投影后生成的二维图形显示在图形输出器的坐标系。

4、规格化设备坐标系（normalized device coordinate system）

目的是为了方便将图形软件应用到不同分辨率的设备，其最大的坐标范围是1。这样当转换到具体的不同输出设备时，只需要将图形的规格化坐标系再乘以相应分辨率即可，增加了图形软件的可移值性。

二、投影

0、投影规范化（projection normalization）

使用平移和绽放变换把相机坐标系下的顶点变换为视景体的内部（${[-1,1]^3}$），即$x,y,z$的取值范围为[-1,1]，该过程称为投影规范化。

（1）定义

$M_{normal}$：规范化矩阵

T：平移矩阵

S：缩放矩阵

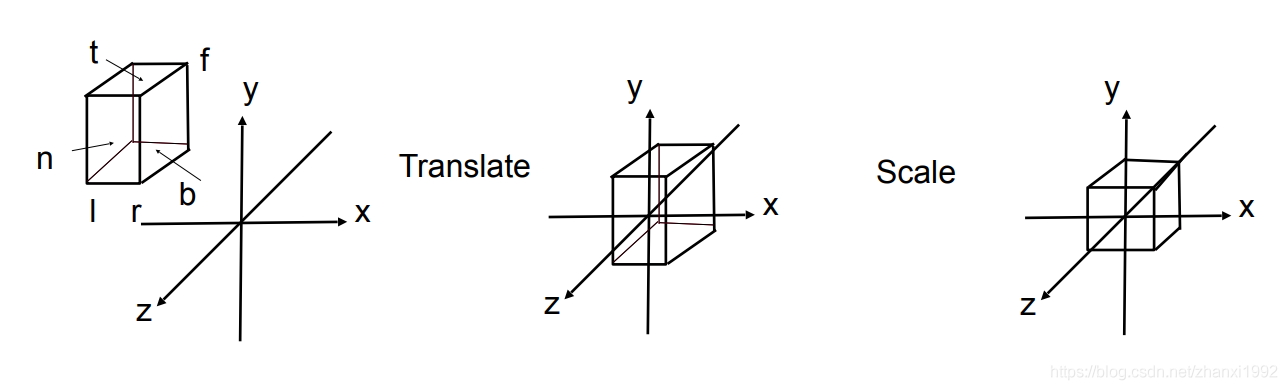
l：最左的坐标，r：最右的坐标

t：最顶的坐标， b：最底的坐标

n：最近的坐标， f：最远的坐标

（2）操作

平移：把中心称到原点。

缩放：使视景体的边长为2.

$M_{normal}=ST$

$M_{normal} =$ $ \begin{equation} \left [ \begin{array}{cccc} \frac{2}{r-l}& 0 & 0 & 0\\ 0& \frac{2}{t-b}&0&0\\ 0& 0& \frac{2}{n-f}& 0\\ 0& 0& 0& 1 \end{array} \right] \left [ \begin{array}{cccc} 1& 0 & 0 & -\frac{r+l}{2}\\ 0& 1&0&-\frac{t+b}{2}\\ 0& 0& 1& -\frac{n+f}{2}\\ 0& 0& 0& 1 \end{array} \right] \end{equation}$

$M_{normal}=
\begin{equation}
\left [
\begin{array}{cccc}
\frac{2}{r-l}& 0 & 0 & -\frac{r+l}{r-l}\\
0& \frac{2}{t-b}&0&-\frac{t+b}{t-b}\\
0& 0& \frac{2}{n-f}& -\frac{n+f}{n-f}\\
0& 0& 0& 1
\end{array}
\right]
\end{equation}$

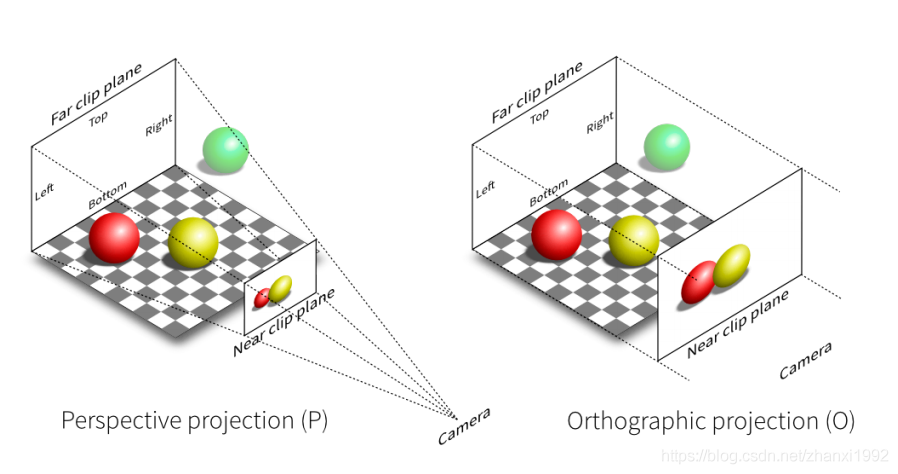
1、投视投影

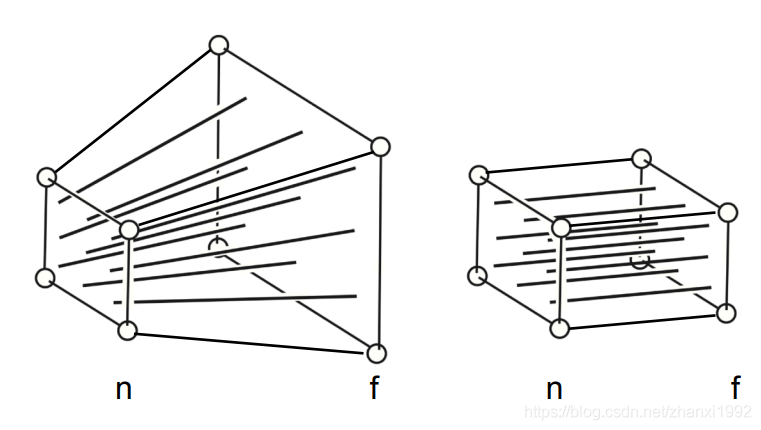
（1）将透视投影的四棱台转换为立方体。

（2）重复正交投影变换

根据相似三角形可得$y^{'}=\frac{n}{z}y$，$x^{'}=\frac{n}{z}x$

$M_{persProj}=M_{orthProj}M_{pers \to orth}=M_{orth}M_{normal}M_{pers \to orth}$

$= \begin{equation} \left [ \begin{array}{cccc} 1& 0 & 0 & 0\\ 0& 1&0&0\\ 0& 0& 0& 0\\ 0& 0& 0& 1 \end{array} \right] \left [ \begin{array}{cccc} \frac{2n}{r-l}& 0 & -\frac{r+l}{r-l} & 0\\ 0& \frac{2n}{t-b}&-\frac{t+b}{t-b}&0\\ 0& 0& \frac{n+f}{n-f}& -\frac{2n}{n-f}\\ 0& 0& 1& 0 \end{array} \right] \end{equation} $

2、正交投影（orthographic projection）

正交投影的投影线垂直于投影平面，其$x,y$坐标保持不变，可得其变换矩阵为

$M_{orth}=$

$\begin{equation} \left [ \begin{array}{cccc} 1& 0 & 0 & 0\\ 0& 1&0&0\\ 0& 0& 1& 0\\ 0& 0& 0& 1 \end{array} \right] \end{equation} $

$M_{orthProj}=M_{orth}M_{normal}$