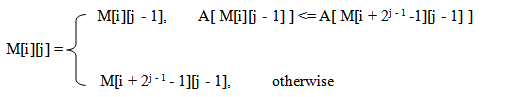阅读数:128 评论数:0

1、RMQ

Range Minimum Query，译为区间最小值查询。其解释就是说：对于含有N个元素的数列A，在数列中找到两个指定索引之间的最小值及最小值的位置。

设有数组A[N]，其表示如下：

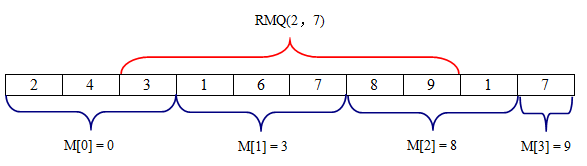
要求求得区间(2,7)的最小元素，如下图所示：

（1）直接遍历区间

看到这个问题之后，我们最先想到的就是对区间的这些数进行一次遍历，就可以找到区间的最值，因此查询的时间为O(M)。但是，当数据量非常大并且查询很频繁时，直接遍历序列的效果就不是那么理想了。因为每查询一次就得对序列做一次遍历，对于大数据量这显然不能满足要求了。不过对于小数据量，这种算法倒是不错的选择！

（2）切割法

首先，我们将序列分成sqrt(N)个部分，用数组M[sqrt(N) ]来表示每个部分中最小的值的下标，即这个最小数的位置。对于数组M，我们只需对原序列进行一次遍历就可以得到M。如下图所示：

接下来我们来求RMQ[2，7]。为了得到区间[2，7]的最小值，我们需比较A[2]，A[M[1]]，A[6]，以及A[7]，并得到他们中最小值的下标。

（3）排序

那么我们可对选择区间的这M个数据进行排序，然后就可以直接得到最小值。但是如果做排序的话，会有很大的缺陷。我们来看看。

分析：我们选择快速排序，O(M * LogM)，但是快速排序会改变序列中数的相对位置，因此用快排的话，为了保证原数据的顺序不变，我们还得用O(M)的空间来维护原序列，因此这样的消耗是很大的。

（4）Sparse Table 算法

ST算法是一种比较高效的在线处理RMQ问题的算法，所谓在线算法，是指每输入一个查询就会马上处理这个查询。ST算法首先会对序列做预处理，完成之后就可以对查询做回答了。

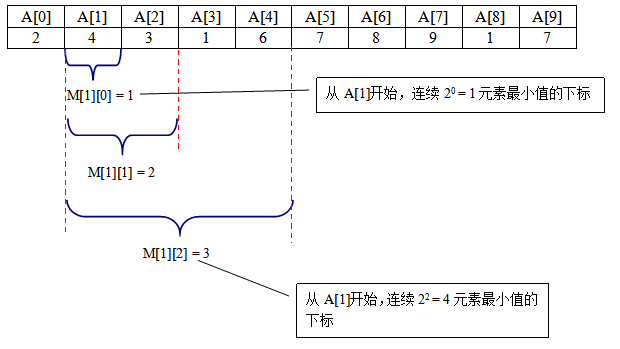
预处理：首先用维护一个数组M[N][LogN]，M[i][j]的值是从原序列A的i位置开始，连续2j 个元素的最小值的下标，如下所示：

那么，我们如何计算M[i][j]呢？ 我们采用DP的思想将区间分成两部分：

（5）线段树

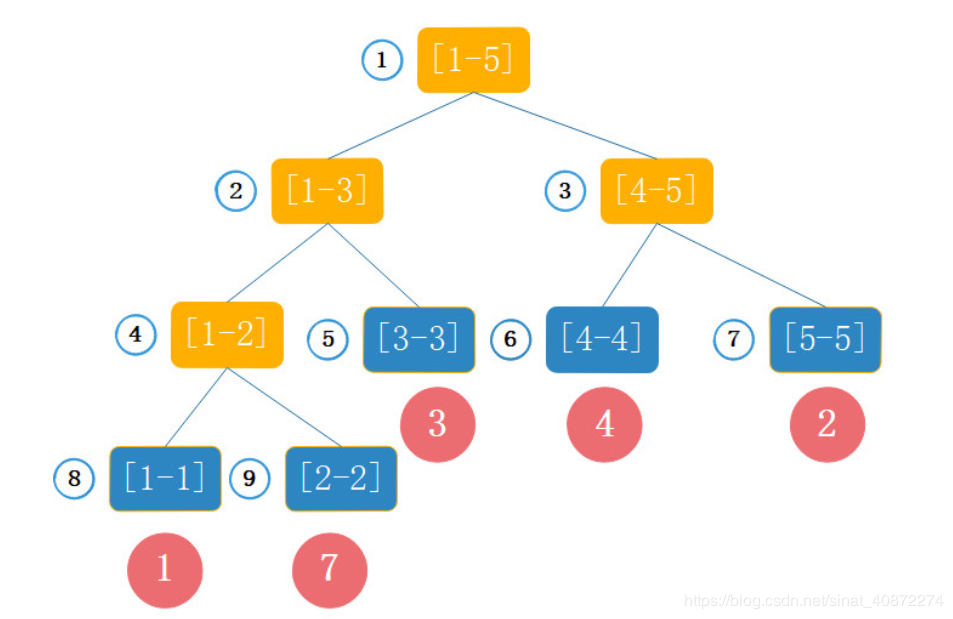
线段树是一颗完全二叉树。比如数组1、7、3、4、2

查询的过程就是一个堆排序的部分过程。

2、LCA

Lowest Common Ancestor，译为最近公共祖先。其解释就是说：在有根树中，找出树中任意两个节点最近的公共祖先，或者说找到任意两个节点离树根最远的公共祖先。

战前准备：

数组T[i]：表示树中某个节点i的父节点；

数组L[i]：表示树中的某个节点i。

维护数组：P[N][LogN]：其中，P[i][j]表示树中i节点的第j个祖先。

实现的过程如下：

（1）如果在同一层，那么我们通过DP思想，不断地求LCA(p = P[p][j]，q = P[q][j])，一旦 p = q就停止，因为此时p和q的父节点是一样的，也就是说我们找到了最近公共祖先。

（2）如果不在同一层，如果p > q，也就是说p相对与q，p在树的更深层。此时，我们仍然通过DP思想来找到q与p的祖先在同一层的节点，即q = p_祖先。接下来就可按照在同一层的做法做了。