阅读数:494 评论数:0

第一章：实数

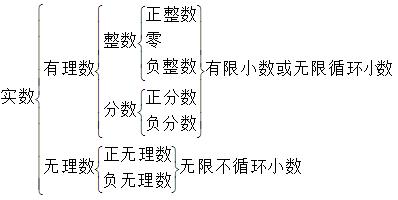
一、实数的分类

1、有理数：任何一个有理数总可以写成$\frac{p}{q}$的形式，其中p、q是互质的整数，这是有理数的重要特征。

2.无理数：无理数：初中遇到的无理数有三种：（1）开不尽的方根，如$\sqrt{2}$、$\sqrt{3}{4}$;（2）特定结构的不循环无限小数，如1.101001000100001...（3）特定意义的数，如$\pi$、$\sin45^\circ$等。

3.判断一个实数的数性不能仅凭表面上的感觉，往往要经过整理化简后才下结论。

二、实数中的几个概念

1、相反数：只有符号不同的两个数叫做互为相反数。

（1）实数a的相反数是-a；（2）a和b互为相反数$\Leftrightarrow$a+b=0

2、倒数：

（1）实数a（a$\not=$0）的倒数是$\frac{1}{a}$;（2）a和b互为倒数$\Leftrightarrow$ab=1

（3）注意0没有倒数

3、绝对值：

（1）一个数的绝值有以下三种情况：$\left\|a\right\|=$ $\begin{cases} a, a>0\\ 0,a=0\\-a,a<0 \end{cases}$

（2）实数的绝对值是一个非负数，从数轴上看，一个实数的绝对值，就是数轴上表示这个数的点到原点的距离。

（3）去掉绝对值符号（化简）必须要对绝对值符号里面的实数进行数性（正、负）确认，再去掉绝对值符号。

4、n次方根

（1）平方根，设$a\geq0$，称$\pm\sqrt{a}$叫做a的平方根，$\sqrt{a}$叫做a的算术平方根。

（2）正数的平方根有两个，它们互为相反数；0的平方根是0；负数没有平方根。

（3）立方根： $\sqrt[3]{a}$叫做实数a的立方根。

（4）一个正数有一个正的立方根；0的立方根是0；一个负数有一个负的立方根。

三、实数与数轴

1、数轴：规定了原点、正方向、单位长度的直线称为数轴。原点、正方向、单位长度是数轴的三个要素。

2、数轴上的点和实数的对应关系：数轴上的每一个点都表示一个实数，而每一个实数都可以用数轴上的唯一的点来表示。实数和数轴上的点是一一对应的关系。

四、实数大小的比较

1、在数轴上表示两个数，右边的数总比左边的数大。

2、正数大于0；负数小0；正数大于一切负数；两个负数绝对值大的反而小。

五、实数的运算

1、加法：

（1）同号两数相加，取原来的符号，并把它们的绝对值相加。

（2）异号两数相加，取绝对值大的加数的符号，并用较大的绝对值减去较小的绝对值。可使用加法交换律、结合律。

2、减法：

（1）减去一个数等于加上这个数的相反数。

3、乘法：

（1）相数相乘，同号取正，异号取负，并把绝对值相乘。

（2）n个实数相乘，有一个数为0，积就为0；若n个非0的实数相乘，积的符号由负因数的个数决定，当负因数有偶数个时，积为正；当负因数为奇数个时，积为负。

（3）乘法可使用乘法交换律、结合律、分配律。

4、除法：

（1）两数相除，同号得正，异号得负，并把绝对值相除。

（2）除以一个数等于乘以这个数的倒数。

（3）0除以任何数都等于0，0不能做被除数。

5、乘方与开方：乘方与开方互为逆运算。

6、实数的运算顺序：乘方、开方为三级运算，乘、除为二级运算，加、减是一级运算，如果没有括号，在同一级运算中要从左到右依次运算，不同级的运算，先算高级的运算再算低级的运算，有括号的先算括号里的运算。无论何种运算，都要注意先定符号后运算。

六、有效数字与科学记数法

1、科学记数法：高N>0，则N=$a\times10^n$（其中$1\leq a\gt10$，n为整数）。

2、有效数字：一个近似数，从左第一个不是0的数，到精确到的数位为止，所有的数字，叫做这个数的有效数字。精确度的形式有两种：（1）精确到哪一位（2）保留几个有效数字。

第二章：代数式

一、代数式

1、代数式：用运算符号把数或表示数的字母连结而成的式子，叫代数式。单独一个数或者一个字母也是代数式。

2、代数式的值：用数值代替代数里的字母，计算后得到的结果叫做代数式的值。

3、代数式的分类：

$\begin{cases} 有理式\begin{cases} 整式 \begin{cases} 单项式\\  多项式\\ \end{cases}\\ 分式\\ \end{cases} \\ 无理式\\\end{cases}$

二、整式的有关概念及运算

1、概念

（1）单项式：像x、7、$2x^2y$，这种数与字母的积叫做单项式。单项一个数或者字母也是单项式。

（2）多项式：几个单项式的和叫做多项式。

（3）同类项：所含字母相同，并且相同字母的指数也分别相同的项叫做同类项。

2、运算

（1）整式的加减：

合并同类项：把同类项的系数相加，所得结果作为系数，字母及字母的指数不变。

去括号法则：括号前面是加号，把括号和它前面的加号去掉，括号里各项都不变；括号前面是减号，把括号和它前面的减号去掉，括号里的各项都变号。

添加括号法则：括号前面是加号，括到括号里的各项都不变；括号前面是减号，括到括号里的各项都变号。

整式的加减实际上就是合并同类项。

（2）整式的乘除：

幂的运算法则：其中m、n都是正整数

同底数幂相乘： $a^m \cdot a^n=a^{m+n}$；同底数幂相除：$a^m\div a^n=a^{m-n}$；幂的乘方：$(a^m)^n=a^{mn}$，积的乘方： $(ab)^n=a^n b^n$。

单项式乘以单项式：用它们系数的积作为积的系数，对于相同的字母，用它们的指数和作为这个字母的指数；对于只有一个单项式里含有的字母，则连同它的指数作为积的一个因式。

单项式乘以多项式：单是用单项式去乘多项式的每一项，再把所得的积相加。

多项式乘以多项式：先用一个多项式的每一项乘以另一个多项式的每一项，再把所得的积相加。

单项除单项式：把系数，同底数幂分别相除，作为商的因式，对于只在被除式里含有的字母，则连同它的指数作为商的因式。

多项式除以单项式：把这个多项式的每一项除以这个单项，再把所得的商相加。

乘法公式：

平方差公式：（a+b）(a-b)=$a^2-b^2$

完成平方公式：$(a+b)^2=a^2+2ab+b^2,(a-b)^2=a^2-2ab+b^2$

三、因式分解

1.因式分解的概念：把一个多项式化成几个整式的积的形式，叫因式分解。

2.常用的因式分解方式：

（1）提取公因式法：ma+mb+mc=m(a+b+c)

（2）运用公式法：平方差公式，完全平方公式

（3）十字相乘法：$x^2+(a+b)x+ab=(x+a)(x+b)$

（4）分组分解法：将多项式的项适当分组后能提公因式或运用公式分解

（5）运用求根公式法：若$ax^2+bx+c=0(a\not=0)$的两个根是$x_1,x_2$，则有：$ax^2+bx+c=a(x-x_1)(x-x_2)$

3、因式分解的一般步骤：

（1）如果多项式的各项有公因式，那么先公因式；

（2）提出公式或无公式可提，再考虑可否运用公式或十字相乘法；

（3）对二次三项式，应先尝试用十字乘法分解，不行的再用求根公式。

（4）最后考虑分组分解法。

四、分式

1、分式定义：形如$\frac{A}{B}$的式子叫分式，其中A、B是整式，且B中含有字母。

（1）分式无意义：B=0时，分式无意义；$B\not=0$时，分式有意义。

（2）分式的值为0：A=0，$B\not=0$时，分式的值等于0。

（3）分式的约分：把一个分式的分子和分母的公因式约去做分式的约分。方法是把分子、分母因式分解，再约去公因式。

（4）最简分式：一个分式的分子与分母没有公因式时，叫做最简分式。分式运算的最终结果若是分式，一定要化为最简分式。

（5）通分：把几个异分母的分式分别分成与原来分式相等的同分母分式的过程，叫做分式的通分。

（6）最简公分母：各分式的分母所有因式的最高次幂的积。

（7）有理式：整式和分式统称有理式。

2、分式的基本性质：

（1）$\frac{A}{B}=\frac{A\cdot M}{B\cdot M}(M是\not=0的整式)$；

（2）$\frac{A}{B}=\frac{A\div M}{B\div M}(M是\not=0的整式)$；

（3）分式的变号法则：分式的分子、分母与分式本身的符号，改变其中任何两个，分式的值不变。

3、分式的运算：

（1）加、减：同分母的分式相加减，分母不变，分子相加减；异分母的分式相加减，先把它们通分成同分母的分式再相加减。

（2）乘：先对各分式的分子、分母因式分解，约分后再分子乘分子，分母乘分母。

（3）除：除以一个分式等于乘上它的倒数式。

（4）乘方：分式的乘方就是把分子、分母分别乘方。

五、二次根式

1、二次根式的概念：式子$\sqrt a（a\geq 0）$叫做二次根式。

（1）最简二次根式：被开方数的因数是整数，因式是整数，被开方数中不含能开得尽方的因式的二次根式叫最简二次根式。

（2）同类二次根式：化为最简二次根式之后，被开方数相同的二次根式，叫做同类二次根式。

（3）分母有理化：把分母中的根号化去掉叫做分母有理化。

（4）有理化因式：把两个含有二次根式的代数相乘，如果它们的积不含有二次根式，我们就说这两个代理式互为有理化因式。

2、二次根式的性质：

（1）$(\sqrt{a})^2=a(a\geq 0)$；

（2）$\sqrt{ab}=\sqrt{a}\cdot \sqrt{b}$ $(a\geq 0,b\geq 0)$

（3）$\sqrt{\frac{a}{b}}=\frac{\sqrt{a}}{\sqrt{b}}$ $(a\geq 0,b\geq 0)$

第三章：方程和方程组

一、方程有关概念

1、方程：含有未知数的等式叫做方程。

2、方程的解：使方程左右两边的值相等的未知数的值叫方程的解，含有一个未知数的方程的解也叫做方程的根。

3、解方程：求方程的解或判断方程无解的过程叫做解方程。

4、方程的增根：在方程变形时，产生的不适合原方程的根叫做原方程的增根。

二、一元方程

1、一元一次方程

（1）一元一次方程的标准形式：ax+b=0（其中x是未知数，a、b是已知数，$a\not=0$）。

（2）一元一次方程的最简形式：ax=b（其中x是未知数，a、b是已知数，$a\not=0$）。

（3）一元一次方程有唯一的一个解。

2、一元二次方程

（1）一元二次方程的一般形式：$ax^2+bx+c=0$（其中x是未知数，a、b、c是已知数，$a\not=0$）

（2）一元二次方程的根判别法：$\triangle=b^2-4ac$

当$\triangle>0$时，方程有两个不相等的实数根。

当$\triangle=0$时，方程有两个相等的实数根。

当$\triangle<0$时，方程有两个实数根。

（3）若$x_1,x_2$是一元二次方程$ax^2+bx+c=0$的两个根，那么：$x_1+x_2=-\frac{b}{a},x_1\cdot x_2=\frac{c}{a}$。

（4）以两个数$x_1,x_2$为根的一元二次方程（二次项系数为1）是：$x^2+(x_1+x_2)+x_1\cdot x_2=0$.

三、分式方程

1、定义：分母中含有未知数的方程叫做分式方程。

2、分式方程的解法：

一般解法：去分母法，方程两边都乘以最简公分母。

特殊方法：换元法。

3、检验方法：一般把未知数的值代入最简公公母，使最简公母不为0的就是原方程的根；使得最简公分母为0 的就是原方程的增根，增根必须舍去，也可以把求得的未知数的值代入原方程检验。

四、方程组

1、方程组的解：方程组中各方程的公共解叫做方程组的解。

2、一次方程组：

（1）二元一次方程组：

一般形式：$\begin{cases}a_1 x+b_1 y=c_1\\ a_2 x+b_2 y=c_2\\ \end{cases}$ ($a_1,a_2,b_1,b_2,c_1,c_2$不全为0)

解法：代入消元法和加减消元法。

解的个数：有唯一的解，或无解，当两个方程相同时有无数的解。

3、二元二次方程组：

解法：消元，转化为解一元二次方程，或者降次，转化为二元一次方程组。

第四章：方程组解应用题

一、方程组解应用题的一般步骤：

1、审题

2、设未知数

3、找出相等关系

4、解方程组

5、检验，作答

二、方程组解应用题常见类型及其等量关系

1、工程问题

（1）基本工作量的关系：工作量=工作效率$\times$工作时间

（2）常见的等量关系：甲的工作量+乙的工作量=甲乙合作的工作总量

（3）注意：工程问题常把总工程看作1，水池注水问题属于工程问题。

2、行程问题

（1）基本量之间的关系：路程=速度 $\times$ 时间

（2）常见等量关系：

相遇问题：甲走的路程+乙走的路径=全路程

追击问题（设甲速度快）：

同时不同地：甲的时间=乙的时间；甲走的路径-乙走的路径=原来甲乙相距路程。

同地不同时：甲的时间=乙的时间-时间差；甲的路程=乙的路径

3、水中航行问题：

顺流速度=般在静水中的速度+水流速度

逆流速度=般在静水中的速度-水流速度

4、增长率问题：

常见等量关系：增长后的量=原来的量+增长的量；增长的量=原来的量$\times$（1+增长率）

第五章：不等式及不等式组

一、不等式与不等式的性质

1、不等式：表示不等关系的式子。

2、不等式的性质：

（1）不等式的两边都加上（或减去）同一个数，不等号方向不改变。

（2）不等式两边都乘以（或除以）同一个正、负数，不等号方向不变。

3、任意两个实数a、b的大小关系

（1）$a-b>0 \Leftrightarrow  a>b$

（2）$a-b=0 \Leftrightarrow a=b$

（3）$a-b<0 \Leftrightarrow a<b$

4、

（1）$a>b>0 \Leftrightarrow \sqrt{a} > \sqrt{b}$

（2）$a>b>0 \Leftrightarrow a^2 > b^2$

第六章：函数及其图像

一、平面直角坐标系

1、平面内有公共原点且互相垂直的两条数轴，构成平面直角坐标系。在平面直角坐标系内的点和有序实数对之间建立了一一对应的关系。

2、不同位置点的坐标的特征：

（1）P(x,y)在第一象限$\Leftrightarrow x>0,y>0$

（2）P(x,y)在第二象限$\Leftrightarrow x<0,y>0$

（3）P(x,y)在第三象限$\Leftrightarrow x<0,y<0$

（4）P(x,y)在第四象限$\Leftrightarrow x>0,y<0$

3、点P(x,y)坐标的几何意义：

（1）点P(x,y)到x轴的距离是|y|

（2）点P(x,y)到y轴的距离是|x|

（3）点P(x,y)到原点的距离是$\sqrt{x^2+y^2}$

4、关于坐标轴、原点对称的点的坐标的特征：

（1）点P(a,b)关于x轴的对称点是$P_1(a,-b)$

（2）点P(a,b)关于y轴的对称点是$P_2(-a,b)$

（3）点P(a,b)关于原点的对称眯是$P_3(-a,-b)$

二、函数的概念

1、常量和变量：在某一变化过程中可以取不同数值的量叫做变量；保持数值不变的量叫做常量。

2、函数：一般地，设在某一变化过程中有两个变量x和y，如果对于x的每一个值，y都有唯一的值与它对应，那么就说x是自变量，y是x的函数。

三、几种特殊的函数

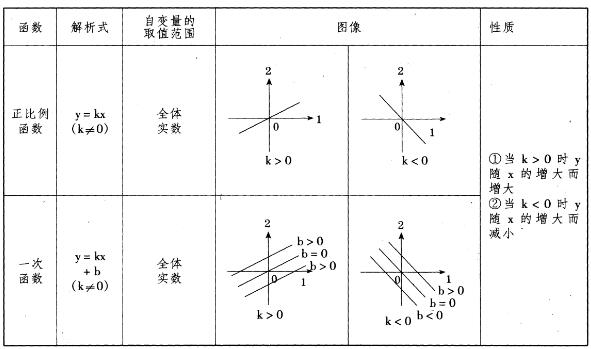
1、一次函数

直线位置与k，b的关系：

（1）k>0直线向上的方向与x轴正方向所形成的夹角为锐角。

（2）k<0直线向上的方向与x轴正方向所形成的夹角为钝角。

（3）b>0直线与y轴交点在x轴的上方。

（4）b=0直线过原点。

（5）b<0直线与y轴交点在x轴的下方。

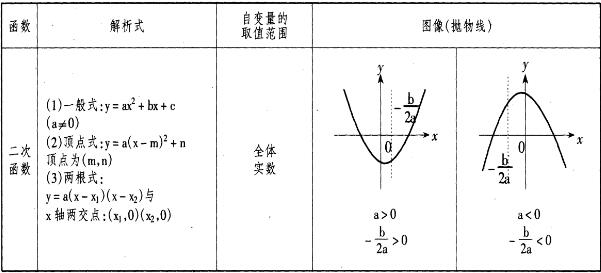
2、二次函数

（1）a决定抛物线的开口方向$\begin{cases}a>0 \Leftrightarrow 开口向上 \\ a<0 \Leftrightarrow 开口向下 \end{cases}$

（2）c决定抛物线与y轴交点的位置

$c>0 \Leftrightarrow 交点在x轴上方；c=0 \Leftrightarrow 交点在原点  ； c<0 \Leftrightarrow 交点在x轴下方$

（3）a，b决定抛物线对称轴的位置：a，b同号，对称轴在y轴的左侧；b=0，对称轴是y轴，a，b异号，对称轴在y轴的右侧。

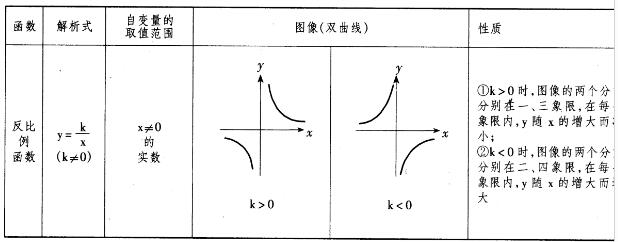
3、反比例函数

第七章：统计初步

一、总体和样本：

在统计时，我们把所要考察的对象的全体叫做总体，其中每一个考察对象叫做个体。从总体中抽取的一部分个体叫体系总体的一个样本，样本中个体的数目叫做样本容量。

二、反映数据集中趋势的特殊数

1、平均数

（1）$x_1,x_2,x_3,...,x_n$的平均数，$\bar{x}=\frac{1}{n}(x_1+x_2+...+x_n)$

2、中位数：将一组数据按从小到大的顺序排列，处于最中间位置上的数据叫做这组数据的中位数，如果数据的个数为偶数中位数就是处于中间位置上两个数据的平均数。

3、众数：在一组数据中，出现次数最多的数据叫做这组数据的众数。

三、反映数据波动大小的特征数

1、方差：

（1）$x_1,x_2,x_3,...,x_n$的方差，$S^2=\frac{(x_1-x)^2+(x_2-x)^2+...,+(x_n-x)^2}{n}$

2、标准差：方差（$S^2$）的算术平方根叫做标准差（S）

四、频率分布

1、有关概念

（1）分组：将一组数据按照统一的标准分成若干组称为分组，当数据在100个以时，通常分成5-12组。

（2）频数：每个小组内的数据的个数叫做该组的频数。各个小组的频数之和等于数据总数n。

（3）频率：每个小组的频数与数据总数n的比值叫做这一小组的频率 ，各小组频率之和为1.

（4）频率分布表：将一组数据的分组及各组相应的频率、频率所列成的表格叫做分布表。