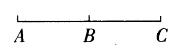阅读数:900 评论数:0

第一章：线段、角、相交线、平行线

一、直线：直线是几何中不加定义的基本概念，直线的两大特征是“直”和“向两方无限延伸”。

二、直线的性质：经过两点有一条直线，并且只有一条直线，直线的这条性质是以公理的形式给出的，可简述为：过两点有且只有一条直线，两直线相交，只有一个交点。

三、射线：

1.射线的定义：直线上一点和它们的一旁的部分叫做射线。

2.射线的特征：“向一方无限延伸，它有一个端点”。

四、线段：

1.线段的定义：直线上两点与它之间的部分叫做线段，这两点叫做线段的端点。

2.线段的性质（公理）：所有连接两点的线中，线段最短。

五、线段的中点:

1、定义如图中，点B把线段AC分成两条相等的线段，点B叫做线段AC的中点。

2、表示法：

$\because AB=BC$

$\therefore 点B为AC的中点$

六、角

1、角的两种定义：一种是有公共端点的两条射线所组成的图形叫做角。

七、角的度量：度量角的大小，可以“度”作为度量单位。把一个圆周分成360等份，每一份叫做一度的角。

八、角的分类：

（1）锐角：小于直角的角叫做锐角。

（2）直角：平角的一半叫做直角。

（3）钝角：大于直角而小于平角的角。

（4）平角：把一条射线，绕着它的端点顺着一个方向旋转，当终止位置和起始位置成一直线时，所成的角叫作平角。

九、相关的角

1、对顶角：一个角的两边是另一个角的两边的反向延长线，这两个角叫做对顶角。

2、互为补角：如果两个角的和是一个平角，这两个角叫做互为补角。

3、互为余角：如果两个角的和是一直角，这两个角叫做互为余角。

十、角的性质

1、对顶角相等。

2、同角或等角的余角相等。

3、同角或等角的补角相等。

十一、相交线

1、两条直线互相垂直：当两条直线相交所成的角是直角时，就说这两条直线互相垂直。

2、垂线：当两条直线互相垂直时，其中的一条直线叫做另一条直线的垂线，它们的交点叫做垂足。

3、垂线的性质

（1）过一点有且只有一条直线与已知直线垂直。

（2）直线外一点与直线上各点连接的所有线段中，垂线段最短。

十二、平行线

1、定义：同一平面内，不相交的两条直线叫做平行线。

2、平行公理：经过直线外一点，有且只有一条直线与这条直线平行。

3、平行公理的推论：如果两条直线都和第三条直线平行，那么这两条直线也互相平行。

第二章：三角形

一、关于三角形的一些概念

由不在同一条直线上的三条线段首尾顺次相接所组成的图表叫做三角形。

组成三角形的线段叫三角形的边；相邻两边的公共端点叫做三角形的项点；相邻两边所组成的角叫做三角形的内角，简称三角形的角。

二、三角形的三条边的关系

三角形三边都不相等，叫不等边三角形；有两条边相等的叫等腰三角形；三边都相等的则叫等边三角形。

等腰三角形中，相等的两条边叫做腰，另一边叫底边，腰和底边的夹角叫底角，两腰的夹角叫顶角。

三角形的两边的差小于第三边，否则不能组成三角形。

三、三角莆的内角和

三角形的内角的和等于$180^{\circ}$。

四、全等三角形

能够完全重合的两个图形叫做全等形。

五、全等三角形的判定

1、边角边公理：有两边和它们的夹角对应相等的两个三角形全等。

2、角边角公理：有两角和其中一边相等的两个三角形全等。

六、等腰三角青菜的性质

等腰三角形的两个底角相等，顶角平分线垂直于底边。

在直角三角形中，如果一个锐角等于$30^{\circ}$，那么它所对的直角边等于斜边的一半。

七：勾股定理

直角三角两直角边a、b的平方和等于斜边c的平方$a^2+b^2=c^2$

逆定理：如果三角形的三边有如上关系，那么这个三角形是直角三角形。

第三章：四边形

一、多边形

1、凸多边形：把多边青菜的任何一条边向两方延长，如果多边形的其他各边都在延长线所在直线的一侧，这样的多边青菜叫凸多边形。

2、n边形的对角线共有$\frac{1}{2} n(n-3)条$

3、n边形内角和定理：n边形内角和等于$(n-2)180^{\circ}$

4、多边形外角和等于$360^{\circ}$

二、平行四边形

1、两组对边分别平行的四边形叫做平行四边形。

2、平行四边形判定定理：

（1）一组边平行且相等的四边形是平行四边形。

（2）两组对边分别相等的四边形是平行四边形。

（3）对角线互相平分的四边形是平行四边形。

（4）两组对角分别相等的四边形是平行四边形。

第四章：相似形

一、比例线段

1、比：选用同一长度单位量得两条线段。a、b的长度分别是m、n，那么就说这两条线段的比是a:b=m:n。

2、比例的基本性质：如果a:b=c:d，那么ad=bc。逆命题也成立。

3、合并性质：如果$\frac{a}{b}=\frac{c}{d}$，那么$\frac{a+b}{b}=\frac{c+d}{d}$

4、等比性质：如果$\frac{a}{b}=\frac{c}{d}=...=\frac{m}{n},(b+d+...+m\not=0)$，那么$\frac{a+c+...+m}{b+d+..+n}=\frac{a}{b}$

5、比例中项：如果比例中两个比例内项相等，即比例$\frac{a}{b}=\frac{b}{c}$，我们把b叫做a和c的比例中项。

6、黄金分割把一条线段分成两条线段，使较长线段是原线段与较短线段的比例中项，叫做把这条线段黄金分割。（$\frac{\sqrt{5}-1}{2}$）.

二、相似三角形

1、三个内角相等，对应边成比例的三角形叫做相似三角形。

2、相似三角形判定定理

（1）两角对应相等，两三角形相似。

（2）如果一个三角形的两条边和另一个三角形的两条边对应成比例，并且夹角相等，那么这两个三角形相似。

（3）如果一个三角形的三条边与另一个三角形的三条边对应成比例，那么这两个三角形相似。

第五章：解直角三角形

一、锐角三角函数

1、锐角的正弦、余弦、正切、余切都叫做$\angle A$的锐角三角函数。

2、$sinA = cos(90^\circ -A)$ 

3、$tanA = cot(90^\circ -A)$

4、同角三角函数关系公式

（1）$sin^2 A +cos^2 B =1$

（2）$tan A = \frac{1}{cotA}$

（3）$tanA = \frac{sin A}{cos A}$

5、一些特殊的三角函数

第六章：圆

一、圆

在一个平面内，线段OA绕它固定的一个端点O旋转一周，另一个端点A随之所形成的圆形叫圆，固定的端点O叫圆心，线段OA叫半径。

二、圆周长、弧长

1、圆周长$C=2\pi R$

2、弧长$L=\frac{n\pi R}{180}$